Stell dir vor, du bist in einem dunklen Wald auf einem Berg verloren, ohne Karte oder Kompass. Was machst du? Du folgst dem Weg des steilsten Abstiegs und gehst Schritte in die Richtung, die das Gefälle verringert und deinem Ziel näherbringt (also ins Tal). Ebenso ist der Gradientenabstieg (gradient descent) der bevorzugte Algorithmus zum Navigieren in der komplexen Landschaft des maschinellen Lernens. Es hilft Modellen, den optimalen Parametersatz zu finden, indem es sie iterativ in die entgegengesetzte Richtung des Gradienten anpasst. In der Welt des maschinellen Lernens und insbesondere des Deep Learning ist der Gradientenabstieg ein unverzichtbares Werkzeug. Es bildet das Rückgrat vieler Optimierungsalgorithmen, die verwendet werden, um die Parameter von neuronalen Netzwerken und anderen Modellen anzupassen, um eine bestimmte Aufgabe zu erfüllen.
Was ist der Gradientenabstieg?
Der Gradientenabstieg ist ein Optimierungsalgorithmus, der in der Regel verwendet wird, um die Parameter eines Modells so anzupassen, dass eine bestimmte Verlustfunktion (Kostenfunktion) minimiert wird. Die Kostenfunktion stellt die Differenz zwischen der vorhergesagten Ausgabe des Modells und der tatsächlichen Ausgabe dar. Das Ziel des Gradientenabstiegs besteht darin, den Parametersatz zu finden, der diese Differenz minimiert und die Leistung des Modells verbessert. Die Verlustfunktion misst also, wie gut oder schlecht das Modell bei der Vorhersage von Ergebnissen ist, und der Gradientenabstieg hilft dabei, die Parameter anzupassen, um diese Vorhersagen zu verbessern.
Wie funktioniert der Gradientenabstieg?
Der Gradientenabstieg funktioniert, indem er die Steigung oder den Gradienten der Verlustfunktion an einem bestimmten Punkt im Parameterbereich berechnet. Der Gradient zeigt die Richtung an, in der die Funktion am steilsten abfällt. Das Ziel des Gradientenabstiegs besteht darin, diesen Gradienten zu nutzen, um die Parameter in Richtung des steilsten Abstiegs zu ändern, so dass die Verlustfunktion minimiert wird.
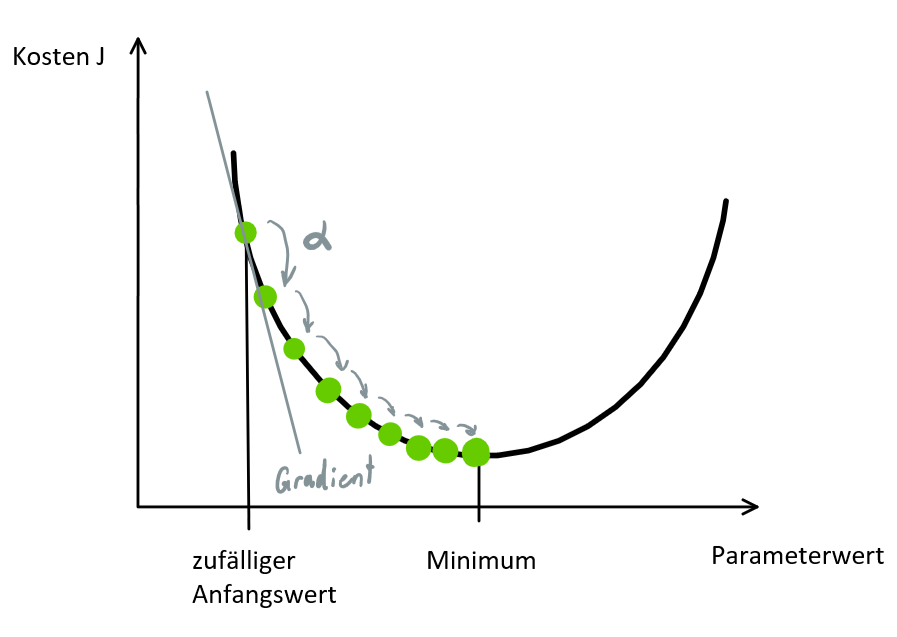
Schrittweise Aktualisierung der Parameter
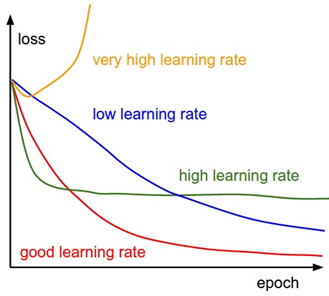
Der Gradientenabstiegsalgorithmus aktualisiert die Parameter des Modells schrittweise, wobei die Größe jedes Schritts durch die Lernrate α (learning rate) bestimmt wird. Die Lernrate ist ein Hyperparameter, der festlegt, wie groß die Schritte bei der Aktualisierung der Parameter sein sollen. Eine zu kleine Lernrate kann dazu führen, dass der Algorithmus zu langsam konvergiert oder in lokalen Minima stecken bleibt, während eine zu große Lernrate dazu führen kann, dass der Algorithmus oszilliert oder über das Minimum hinausschießt. Durch die iterative Aktualisierung der Modellparameter in negativer Gradientenrichtung nähert sich der Gradientenabfall allmählich dem optimalen Parametersatz an, der die niedrigsten Kosten verursacht.
Der Gradientenabstieg kann auf verschiedene Algorithmen für maschinelles Lernen angewendet werden, darunter lineare Regression, logistische Regression, neuronale Netze und Support-Vektor-Maschinen. Es bietet einen allgemeinen Rahmen für die Optimierung von Modellen durch iterative Verfeinerung ihrer Parameter basierend auf der Kostenfunktion.
Zurück zum Beispiel auf dem Gipfel eines Berges. Um den tiefsten Punkt des Berges erreichen, machen wir von unserer Position aus, einen Schritt in die absteigende Richtung und wiederholen diesen Vorgang, bis wir den tiefsten Punkt erreichen.
Der Gradientenabstieg ist ein iterativer Optimierungsalgorithmus zum Finden des lokalen Minimums einer Funktion.
Um das lokale Minimum einer Funktion mithilfe des Gradientenabstiegs zu ermitteln, müssen wir Schritte ausführen, die proportional zum Negativ des Gradienten (vom Gradienten weg) der Funktion am aktuellen Punkt sind. Wenn wir Schritte machen, die proportional zum Positiven des Gradienten sind (in Richtung des Gradienten), nähern wir uns einem lokalen Maximum der Funktion und der Vorgang wird Gradientenaufstieg genannt.
Berechnung des Gradientenabstiegs
Die Berechnung führen wir iterativ in zwei Schritten durch:
- Berechnung des Gradienten (Steigung) – die Ableitung erster Ordnung der Funktion an diesem Punkt
- Schritt (Bewegung) in die entgegengesetzte Richtung zur Steigung. Die entgegengesetzte Steigungsrichtung erhöht sich vom aktuellen Punkt aus um das α-fache der Steigung an diesem Punkt
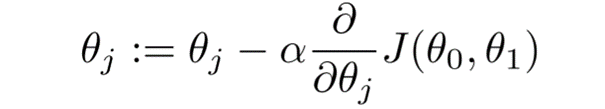
θ…Parameter
α…Lernrate
J…Kostenfunktion
Arten des Gradientenabstiegs
Es gibt verschiedene Varianten des Gradientenabstiegs, darunter den Batch-Gradientenabstieg (BGD) und den stochastischen Gradientenabstieg (SGD). Beim Batch-Gradientenabstieg werden alle Trainingsdaten verwendet, um den Gradienten der Verlustfunktion zu berechnen, während beim stochastischen Gradientenabstieg nur eine zufällige Auswahl von Trainingsdaten verwendet wird. Der stochastische Gradientenabstieg ist oft schneller, da er weniger Rechenaufwand erfordert, aber der Batch-Gradientenabstieg konvergiert oft stabiler. Eine effiziente Implementierung des Gradientenabstiegs ist für die Erzielung einer guten Leistung bei maschinellen Lernaufgaben unerlässlich. Die Wahl der Lernrate und der Anzahl der Iterationen kann die Leistung des Algorithmus erheblich beeinflussen.
Herausforderungen des Gradientenabstiegs
- Lokale Optima: Der Gradientenabstieg kann zu lokalen Optima statt zum globalen Optimum konvergieren, insbesondere wenn die Kostenfunktion mehrere Spitzen und Täler aufweist.
- Auswahl der Lernrate: Die Wahl der Lernrate kann die Leistung des Gradientenabstiegs erheblich beeinflussen. Wenn die Lernrate zu hoch ist, kann der Algorithmus das Minimum überschreiten, und wenn sie zu niedrig ist, kann es zu lange dauern, bis der Algorithmus konvergiert.
- Überanpassung (Overfitting): Der Gradientenabstieg kann zu einer Überanpassung der Trainingsdaten führen, wenn das Modell zu komplex oder die Lernrate zu hoch ist. Dies kann zu einer schlechten Generalisierung bei neuen Daten führen.
- Konvergenzrate: Die Konvergenzrate des Gradientenabstiegs kann bei großen Datensätzen oder hochdimensionalen Räumen langsam sein, was den Algorithmus rechenintensiv machen kann.
Zusammenfassung
Beim Gradientenabstieg handelt sich um einen Optimierungsalgorithmus, der zur Minimierung der Kostenfunktion eines Modells verwendet wird. Die Kostenfunktion misst, wie gut das Modell zu den Trainingsdaten passt, und wird basierend auf der Differenz zwischen den vorhergesagten und den tatsächlichen Werten definiert. Die Steigung der Kostenfunktion ist die erste Ableitung nach den Modellparametern und zeigt in Richtung des steilsten Anstiegs.
Der Algorithmus beginnt mit einem anfänglichen Parametersatz und aktualisiert ihn in kleinen Schritten, um die Kostenfunktion zu minimieren. In jeder Iteration des Algorithmus wird der Gradient der Kostenfunktion in Bezug auf jeden Parameter berechnet. Die Steigung gibt uns die Richtung des steilsten Anstiegs an, und wenn wir uns in die entgegengesetzte Richtung bewegen, können wir die Richtung des steilsten Abstiegs ermitteln. Die Größe der Schritte wird durch die Lernrate gesteuert, die bestimmt, wie schnell sich der Algorithmus dem Minimum nähert. Der Vorgang wird wiederholt, bis die Kostenfunktion gegen ein Minimum konvergiert, was anzeigt, dass das Modell den optimalen Parametersatz erreicht hat.